قضیهی اول: یک خط و یک دایره بر هم مماس اند اگر و تنها اگر این خط در نقطهی تماس با دایره بر شعاع آن نقطه عمود باشد.
قضیه دو شرطی میباشد بنابراین دو قسمت را باید اثبات کرد.
الف: اگر خطی بر دایره مماس باشد آنگاه آن خط بر شعاع محل تماس عمود است.
اثبات: چون خط بر دایره مماس است، طبق تعریف خط مماس، این خط دایره را تنها در یک نقطه قطع می کند؛ بنابراین نقطهی تماس، روی دایره و باقی نقاط، بیرون دایره قرار دارند. میدانیم که فاصلهی سایر نقاط تا مرکز دایره از شعاع بیشتر است و فاصلهی نقطهی تماس دایره با خط تا مرکز دایره، برابر شعاع دایره است (صفحهی ده). اگر از مرکز دایره بر خط مماس عمود کنیم، پای عمود همان محل تقاطع خواهد بود، زیرا فاصلهی این نقطه تا مرکز دایره کمترین فاصله است (یادآوری صفحهی ده). بنابراین اگر F نقطهای روی دایره باشد، شعاع OF و خط مماس بر دایره در نقطهی F بر هم عمود هستند.
OF = R , OA > R → .کوتاه ترین پاره خط است OF →
.بر هم عمود هستند d و OF
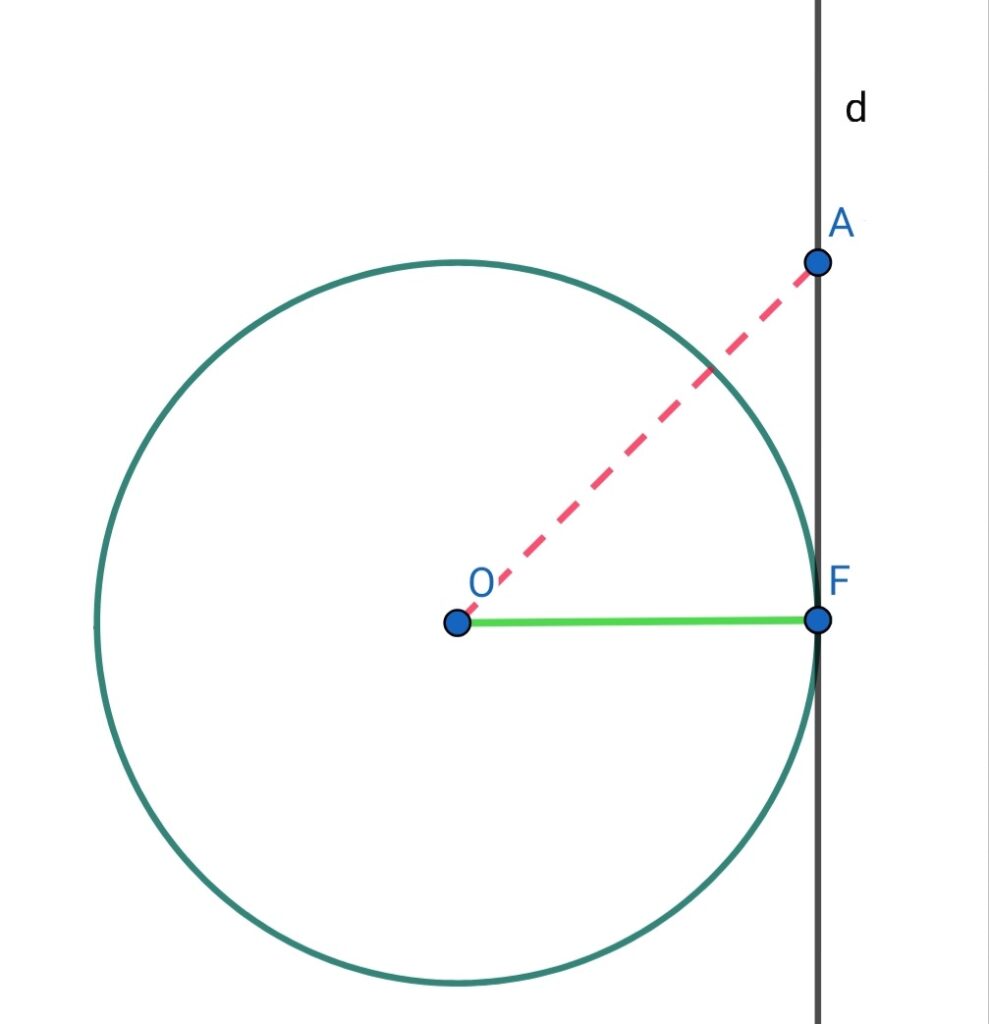
ب: یک خط و یک دایره بر هم مماساند اگر این خط در نقطهی تماس با دایره بر شعاع آن نقطه عمود باشد.